校对 | 酱番梨 整理 | 菠萝妹

原文链接：

深度强化学习从入门到大师：以 Cartpole 和 Doom 为例介绍策略梯度 （第四部分）

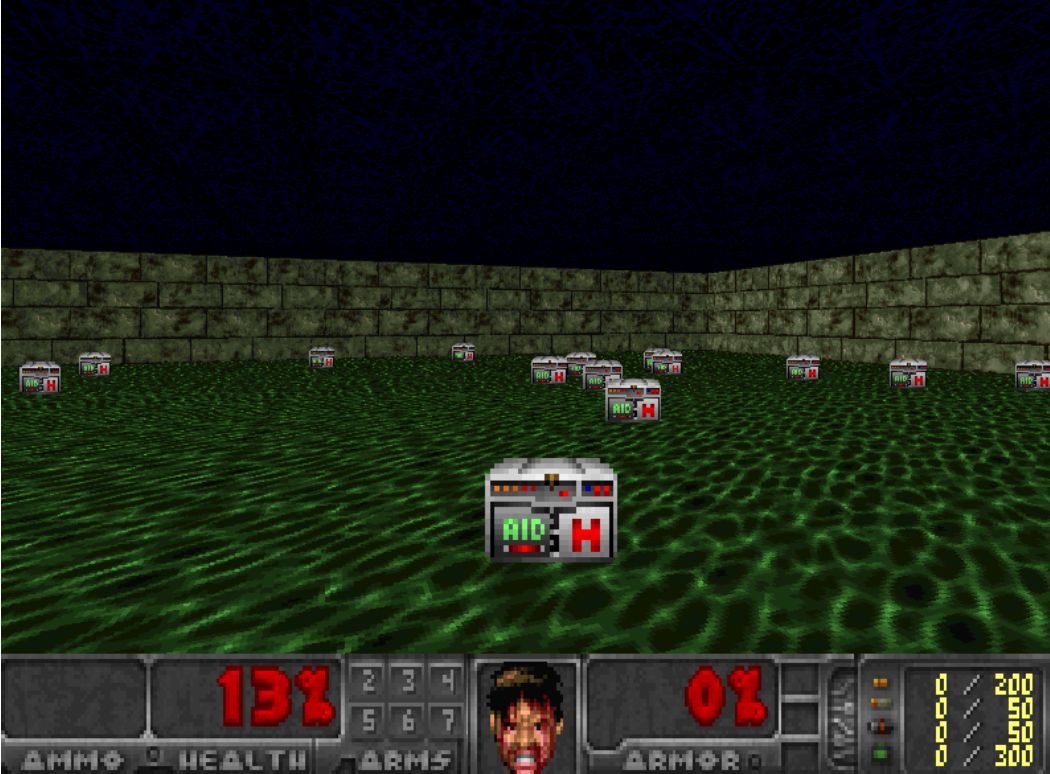
本文的环境

本文是利用Tensorflow进行深度强化学习课程的一部分。点击这里查看教学大纲。

在过去的两篇关于Q-学习和深度Q学习的文章中，我们完成了基于价值的强化学习算法学习。在给定一个状态下，我们选择有最高Q值（在所有状态下最大的期望奖励）的行动。因此，在基于价值的学习中，一个策略存在仅仅出于这些行动价值的评估。

今天，我们将学习名为策略梯度的基于策略的强化学习技术。我们将应用两个智能体。其中一个将学习保持木条平衡。

第二个智能体学习在毁灭战士系列的有敌意的环境中通过收集生命值而生存。

在基于策略的方法中，不同于学习能告诉我们给定状态和行动下奖励总和的价值函数，我们直接学习能使得状态映射到行为的策略函数（不通过价值函数选择行动）。

这意味着我们不通过价值函数试错而直接尝试优化策略函数π，直接参数化π（不通过价值函数选择行动）。

当然，我可以通过价值函数来优化策略参数。但是价值函数将不再用来选择行动。

本文将学习如下内容：

策略梯度是什么，它的优点和缺点；

怎么将其应用于Tensorflow。

为何要使用策略函数

两种类型的策略：确定的或随机的。

一个确定的策略能将状态映射到行为上。输入一个状态，函数将反馈一个要执行的行为。

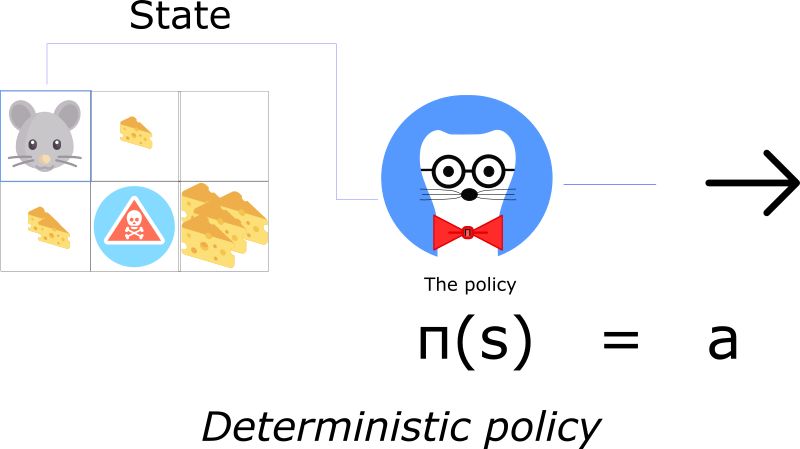
确定的策略用在确定的环境，行动执行的环境决定了结果，不存在不确定性。例如，当你下国际象棋把兵从A2移到A3时，你是确定你的兵要移到A3。

另一方面，一个随机的策略输出一个行为集可能的指派。

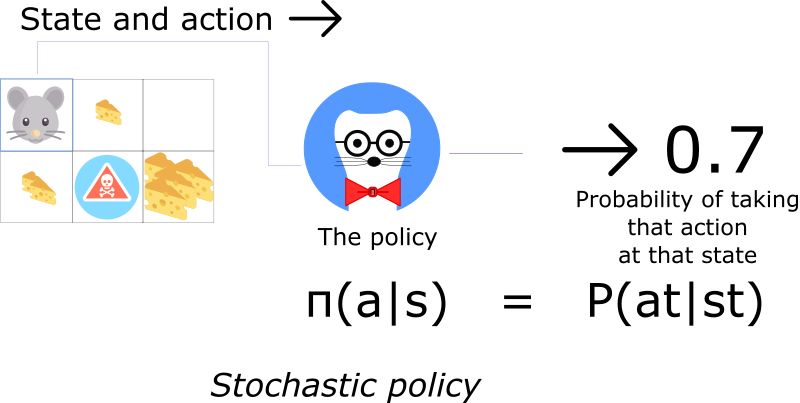
这意味着不是确定地选择行为a，而是我们有可能能选择不同的（例子中30%的可能，我们选择南）。

随机策略用在环境不确定的情况下。这一个过程也叫部分可测马尔科夫决策过程（POMDP）。

大多数情况下，我们使用第二种策略类型。

优势

深度Q学习已经很厉害，为什么要用策略强化学习方法？

深度学习在使用策略梯度时有三大主要优势：

收敛

策略函数有更好的收敛特性。价值函数在训练时有个问题就是大的震荡。这是因为行为的选择在测算的行为值中可能会戏剧性地任意变小。

另一方面，利用策略梯度，我们仅是循着梯度寻找最佳值。一个平滑的更新出现在每一步中。

由于循着梯度寻找最佳值，我们确保收敛于局部最大值（最坏的情况）或是全局最大值（最好情况）。

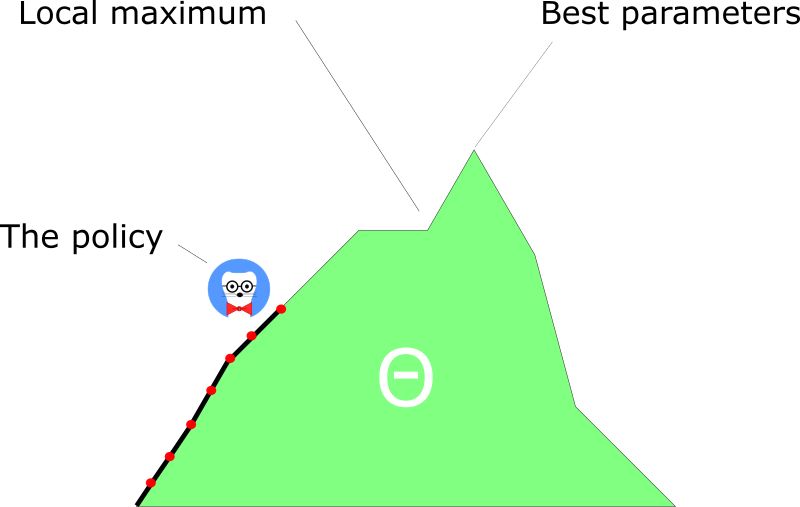
策略梯度在高维空间更有效

第二个优势是策略梯度在高维空间或是连续行动时更有效。

深度Q学习的一个问题是它在每一步的预测中对给定当前状态的每一个可能行为分配一个分值（最大化预测将来的奖励）。

但如果是无限可能的行动呢？

例如，在自动驾驶时，在每一个状态中，可能会有近乎无限行为的选择。（调整车轮15°,17.2°, 19,4°,鸣笛…）。我们需要为每一个行动输出一个Q值。

另一方面，在策略函数中，要直接调整参数（你将要理解什么是最大值），而不是在每一步估算最大值。

策略梯度能学习随机策略

第三个优势是策略梯度能学习随机策略，而价值函数不能。这也导致两个结果。

其一，我们不需要应用探测和开发的权衡。一个随机策略允许智能体在状态空间探索而不是一直采用相同的行为。这是因为它输出一个行为集上的概率分布。其结果是它将处理探测和开发的权衡而不是硬编码。

我们同样去除感知混淆的问题，它是说我们在两个看起来（或实际上）相同的状态，却需要不同的行为。

例如，我们有一个智能吸尘器，它的目标是吸掉灰尘和避免杀死仓鼠。

这个例子被David Silver的精美课程所引出：

我们的吸尘器仅能检测到墙在哪里。

问题：两个红色的方格是相似的状态，因为智能体都能感知到两面上下部的墙。

在确定的策略下，在红色的状态下，智能体选择要么是往右，要么往左，都可能导致智能体被卡住而不能吸尘了。

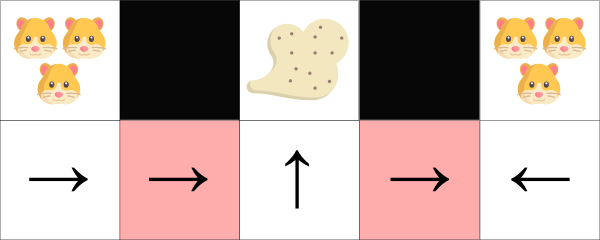
在基于价值的强化算法，我们学习一个准确定性策略（?贪婪策略）。其结果是智能体在找到灰尘前会花费大量时间。

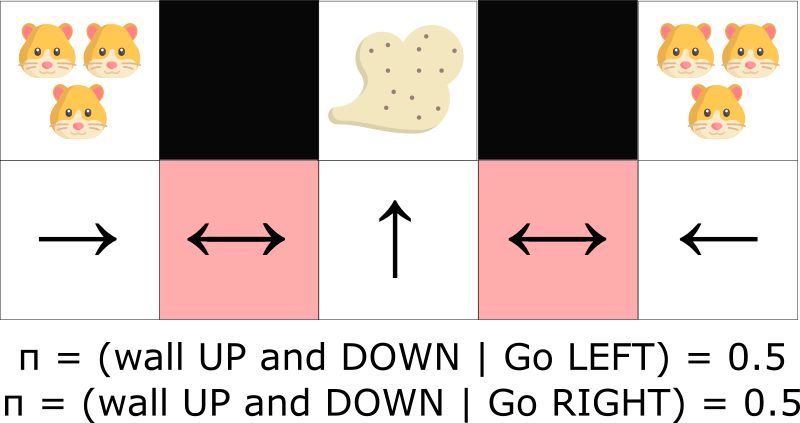
另一方面，一个优化的随机策略在灰色的格子中时将随机往左或往右移动。其结果是智能体不会被卡住，并能在最大可能的情况下达到目标状态。

劣势

策略梯度有个天然的大劣势。在绝大多数情况下，它将在收敛于局部最大值而不是全局最大值。

策略梯度收敛一步一步收敛非常慢，需要很长时间来训练，这不同于同样努力寻求全局最大值的深度Q学习。

尽管如此，我们将看到问题的解决方案。

策略选择

带参数θ的策略π输出行动集的概率分布。

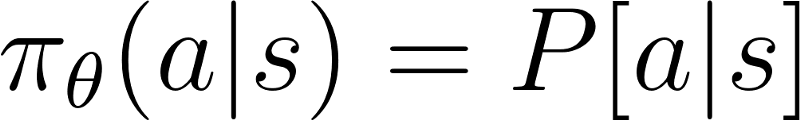
给定状态S，采取带参θ行动a的概率

可怕的是我们怎样才能知道我们的策略是好的呢？

记住策略可被看做是优化问题。我们必须寻找到最佳参数（θ）来最大化得分函数J(θ)。

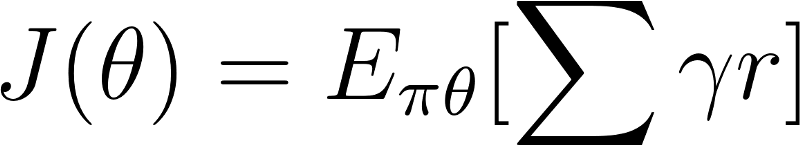
这里有两步：

利用策略评分函数J(θ)来测量π（策略）的质量。

使用策略梯度上升来找寻最佳参数θ来改进π。

这里的主要思想是J(θ)来告诉我们的策略π有多好。策略梯度上升将帮助我们发现最佳策略参数来最大化良好行动的采样。

第一步：策略评分函数J(θ)

为测量我们的策略有多好，我们使用目标函数（或策略评分函数）来计算期望的策略奖励。

有三种等价的方法来优化策略。选择仅仅取决于环境和目标。

首先，在一个情景的环境中，我们取一个开始值，并计算从第一步（G1）开始反馈的均值。这是第整个情景的累积的贴现奖励。

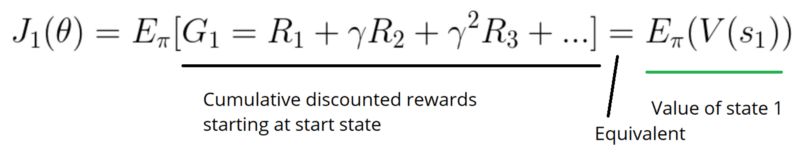
思想很简单，即如果我一直从状态s1开始，从开始状态到结束状态的整体奖励是多少呢？

我们要寻找最大化G1的策略，因为它将是最优的策略，可参见第一篇文章中解释过的奖励假设。

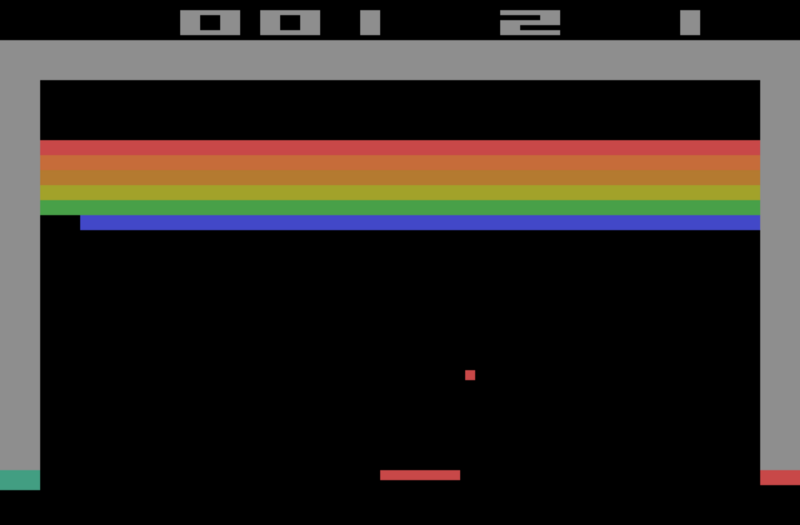
例如，在突围游戏中，我新玩了一局，但我在破坏了20块砖后丢失了球（游戏结束）。新的情景始终从相同的状态开始。